Warning: Undefined array key "id" in /var/www/vhosts/mariusebertsblog.com/httpdocs/mariusebertsblog/wp-content/plugins/advanced-responsive-video-embedder/php/Video.php on line 407
IHK-Prüfung entschlüsselt (Äquivalenzziffernkalkulation Teil 1)
Hallo, herzlich willkommen. Mein Name ist Marius Ebert, und in diesem Video beschäftigen wir uns mal mit der Äquivalenzziffernkalkulation.
Äquivalenzziffernkalkulation. Das gehört in die Kostenträger-Rechnung, also die Frage: „Wofür sind die Kosten angefallen? Was kostet das einzelne Produkt?“ Und es gehört im Rahmen der Kostenträger-Rechnung zur Divisions-Kalkulation.
Grundform der Divisions-Kalkulation (Äquivalenzziffernkalkulation Teil 1)
Die Divisions-Kalkulation sieht ja in ihrer einfachsten Form so aus:
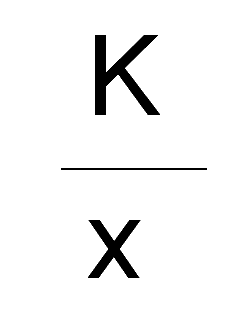
K durch x.
Das heißt: Man braucht im Grunde gar keine Kostenarten und auch keine Kostenstellen-Rechnung, sondern die Kosten hier im Zähler werden völlig undifferenziert, also nicht differenziert nach fix und variabel oder nach Einzel- und Gemeinkosten, dividiert durch die Stückzahl, und wir erhalten die Kosten pro Stück – genau das, was wir in der Kostenträger-Rechnung ermitteln wollen.
Sonderform der Divisions-Kalkulation (Äquivalenzziffernkalkulation Teil 1)
Die Äquivalenzziffernkalkulation kommt nun ins Spiel, wenn wir Sorten haben. Sorten sind Varianten eines Grundproduktes, also Flip-Chart-Stifte zum Beispiel, ein blauer, ein grüner, ein gelber.
Das heißt: Wir haben hier oben im Zähler die Kosten, und hier haben wir (im Nenner) die Variante x1 plus die Variante x2 plus die Variante x3. Alles ist x, also alles sind Flip-Chart-Stifte, nur dass eins ist von mir aus Rot, das ist Gelb, das ist Grün.
Und was wir nun tun bei der Äquivalenzziffernkalkulation ist, den Nenner gleichnamig machen. Gleichnamig, das heißt: Wir rechnen um auf die Mengeneinheiten einer sogenannten Bezugssorte.
Und wie das geht, das folgt im zweiten Video.
IHK-Prüfung entschlüsselt (Äquivalenzziffernkalkulation Teil 1)
Bis gleich.
Danke.
© Dr. Marius Ebert
