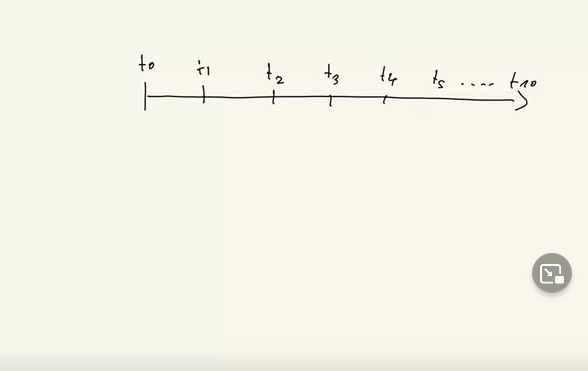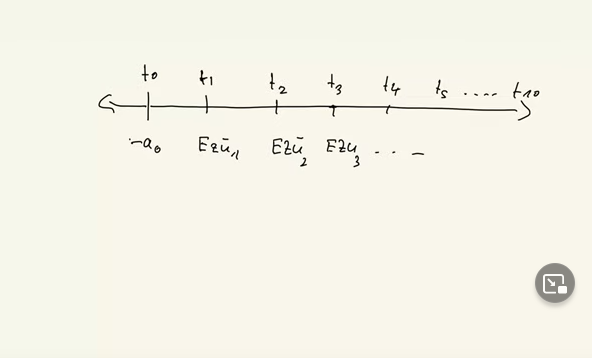Willkommen zurück. Mein Name ist Marius Ebert. Ich setze jetzt mal voraus, weil wir schon in Teil vier sind, das Sie die anderen Teile geschaut haben. Ich will jetzt nichts mehr neu aufgreifen, sondern nur kurz sagen Muster lernen erkläre ich gerade am Beispiel des Kapitalwertes. Der Kapitalwert besteht im Prinzip aus vier Schritten, vier Mustern, von denen es Varianten gibt. Erstens der Kapitalwert arbeitet mit Zahlungen, nicht mit Kosten. Das ist ein Muster, das man erkennen muss.
Hier gibt es verschiedene Varianten, was man hier machen kann. Vielleicht mache ich hier noch ein spezielles Video. Einen guten Teil habe ich im Teil eins erklärt. Der zweite Schritt ist, dass man erkennt, dass man dann den Zahlenstrahl braucht als Ermächtigungsinstrument, um die Zahlenangaben zu verarbeiten. Als Drittes braucht man eine gewisse Rechentechnik, das heißt entweder man muss in einer Tabelle mit Zeilen Spalten Schema den entsprechenden Zinsungsfaktor finden oder man muss mit dem Taschenrechner operieren.
Das hat sich in den 25 Jahren, wo ich hier Leute schule, Leute zu Abschlüssen bringe wie Betriebswirt und Wirtschaftsfachwirt usw sind das so Modeerscheinungen Mal ist es der Taschenrechner, mal sind es wieder Tabellen als Hilfsmittel, mal ist es eine Formelsammlung. Wie auch immer. Ja, und als Viertes muss man dann ein Ergebnis, eine Entscheidung, das Ergebnis ist hier eine Entscheidung, muss man ableiten. So, und jetzt habe ich gesagt, ich habe Varianten des Zahlenstrahls erklärt. Ich habe mindestens eine Variante von Zahlungen erklärt.
Ich will in diesem Video ein bisschen was von Varianten zur Rechentechnik sagen. Das ist also das Thema des Videos Varianten sozusagen bei der Rechentechnik. Wenn wir uns jetzt mal unser Ermächtigungsinstrument, den Zahlenstrahl vornehmen, dann, wie ich in Teil drei erklärt habe, ist es in der Regel, aber nicht immer ausschließlich ist es T0 und alles, was sich dann abspielt, spielt sich rechts von T0 ab. Eine Variante von dieser Zahlenstrahlgeschichte habe ich im Teil drei erklärt.
So jetzt gibt es dann T1, es gibt T2, es gibt T3, es gibt aber möglicherweise auch noch T4, T5 und möglicherweise geht das hier bis T10 und das ist immer eine Frage, ist auch eine Variante eines Musters. Der Zahlenstrahl ist immer gleich, aber wie lang der ist, ist eine Frage der Variante der Aufgabenstellung. Wenn man das Muster erkannt hat, dass es um Zahlenstrahl geht, kann einem egal sein, ob der Zahlenstrahl auch mal in diese Richtung geht und ob der hier nur bis T gleich 3 geht oder bis gleich T10.
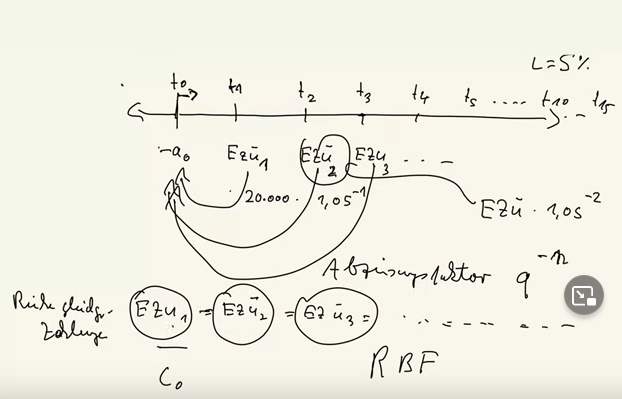
Das grundlegende Muster ist der Zahlenstrahl, der Rest sind Varianten. Nein, das meine ich damit Muster lernen, nicht Aufgaben. Na, da fliegen Sie nämlich aus der Bahn. Einmal haben Sie dann nur drei Perioden, dann beim nächsten Mal haben Sie zehn Perioden und dann wissen Sie wieder nicht, was los ist, weil Sie das Muster nicht verstanden haben. In T0 haben wir immer minus A0 die Auszahlung und dann sollten wir die Zahlen, die Zahlungen so verrechnen, dass wir dann entsprechend die Einzahlungsüberschüsse haben.
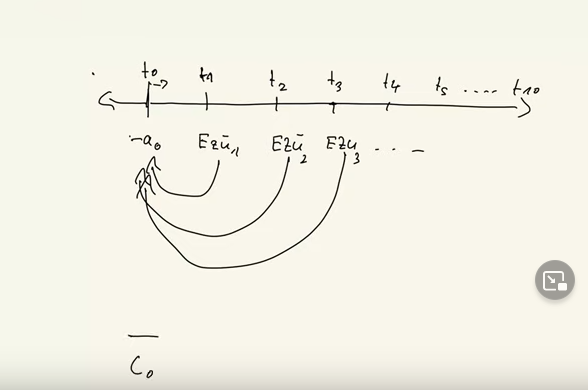
Einzahlungsüberschüsse 1, Einzahlungsüberschüsse 2, Einzahlungsüberschüsse von 3 und so weiter und so weiter. Genau habe ich es in den vorherigen Teilen erklärt. So, dann lautet das Prinzip alles auf T0 abzinsen, wenn sich alles nur rechts von T0 abspielt. Wenn wir mal was haben links von T0 müssen wir aufzinsen. Das heißt im Prinzip, wenn man genau formuliert, bedeutet Kapitalwert alles auf T0 zinsen entweder auf, selten aber kommt vor wesentlich abzinsen. Das heißt, dass wir abzinsen für eine Periode, dass wir abzinsen für zwei Perioden, dass wir abzinsen für drei Perioden, dann miteinander verrechnen.
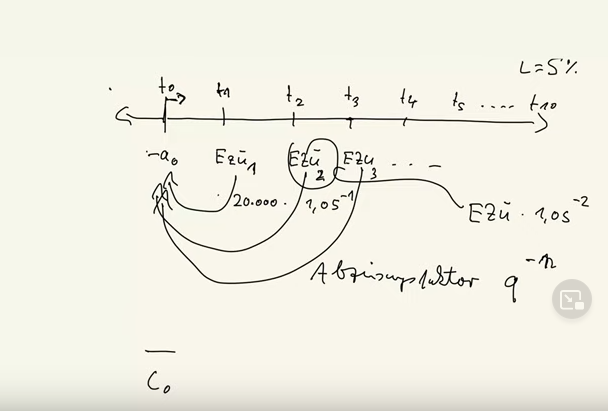
Dann hat man den Kapitalwert und dann kann man zur Entscheidung kommen. So, das ist Rechentechnik, welche Varianten gibt es hier. Der entscheidende Faktor ist zunächst einmal, wenn man rechts von T0 ist, ist der Abzinsungsfaktor. Und der Abzinsungsfaktor Q hoch -N Q gleich eins plus I. Das N ist dann jeweils hier ist es eins oder zwei oder drei und immer Minus davor. Das heißt, wenn hier jetzt zum Beispiel ein Einzahlungsüberschuss von, sagen wir, 20.000 steht Euro, also eine Geldeinheit, dann brauchen wir unseren Zinssatz I dieser Zinssatz I ist in der Regel angegeben, sagen wir, es ist 5 %, dann müssen wir die 2000 abzinsen mal 1,05 hoch -1 und den Einzahlungsüberschuss von Periode zwei müssen wir multiplizieren mit 1,05 hoch -2.
Das ist die Rechentechnik. Dafür muss man sich ein bisschen mit seinem Taschenrechner auskennen. Dann muss man wissen, was die Exponentialtaste ist und was die Vorzeichenwechseltaste ist, wenn man Plus und Minus umtauschen kann. Was ist die Variante? Die Variante ist, dass Einzahlungsüberschuss eins gleich Einzahlungsüberschuss zwei ist gleich Einzahlungsüberschuss drei und das Ganze über mindestens zehn oder 15 Perioden gleich bleibt.
Dann haben wir eine Reihe gleich großer Zahlungen und Achtung die Rechenvariante, die ich jetzt erkläre, kann man nur anwenden, wenn das hier gilt ein Einzahlungsüberschuss 1, Einzahlungsüberschuss 2, Einzahlungsüberschuss 3 und alle Folgenden, mit denen man rechnet, gleichgroß sind. Ja, dann haben wir eine Rente. Und dann ist der entscheidende Faktor, der einfach Zeit spart, der Rentenbarwertfaktor.
Der Rentenbarwertfaktor. Ja, sonst muss man nämlich, sagen wir mal, das geht hier bis T15 muss man mich 15 Zahlen, 15 Einzahlungsüberschüsse einzeln abzinsen. Und da verliert man Zeit, wenn man die Variante erkennt, dass man, wenn man und nur wenn man eine Reihe gleich großer Zahlungen hat, das heißt, die Einzahlungsüberschüsse alle gleich sind. Dieses Gleichheitszeichen ist das Entscheidende und dann mit dem Rentenbarwertfaktor arbeiten kann und dann nur eine Rechenoperation hat statt 15, dann hat man die Variante erkannt, hat sie klug angewendet und hat Zeit gespart, während die, die die Aufgabe auswendig lernen, mal wieder völlig verloren sind und hier wahrscheinlich immens viel Zeit verlieren.
Ja, man kann sagen, je länger das hier geht, desto eher besteht bei der Aufgabenstellung eine Tendenz, diese Einzahlungsüberschüsse gleich hoch zu machen wenn natürlich der letzte Einzahlungsüberschuss nimmt, waren es in 10 Perioden und in Periode 10 kommt dann noch zu Einzahlungsüberschuss 10, der gleich groß ist wie Einzahlungsüberschuss 9 und der wiederum gleich groß ist wie alle vorherigen. Kommt dann noch der Restverkaufserlös dazu, dann hat man hier Einzahlungsüberschuss von 10 genauso groß wie die anderen plus den Restverkaufserlös.
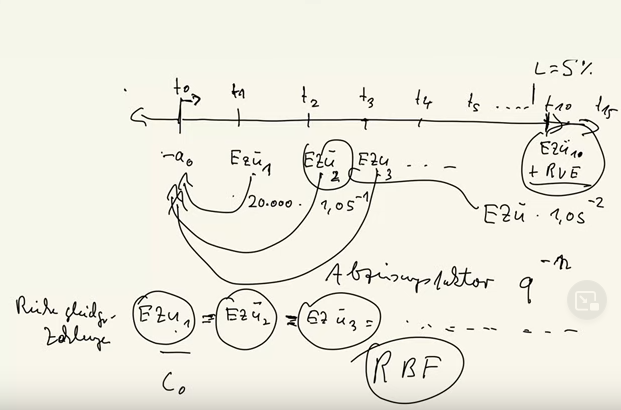
Dann kann man gleichwohl für 9 Perioden mit dem Barwertfaktor arbeiten und das hier separat für 10 Perioden abzinsen, dann hat man trotzdem sehr viel Zeit gespart. Man hat dann zwei Rechenoperationen, weil man das Prinzip verstanden hat. Kann man hier den ökonomischen Weg wählen, was die Rechenoperationen angeht. Aber das gilt wieder nur, wenn man verstanden hat Muster lernen, nicht Aufgaben. Alles Gute Marius Ebert